The Optimal Pattern
The following is a bunch of math to determine exactly how tight a visual pattern can be flown depending on different conditions, and still be stable at 1000' AGL.
Where is 1000’ on a 3° glideslope?
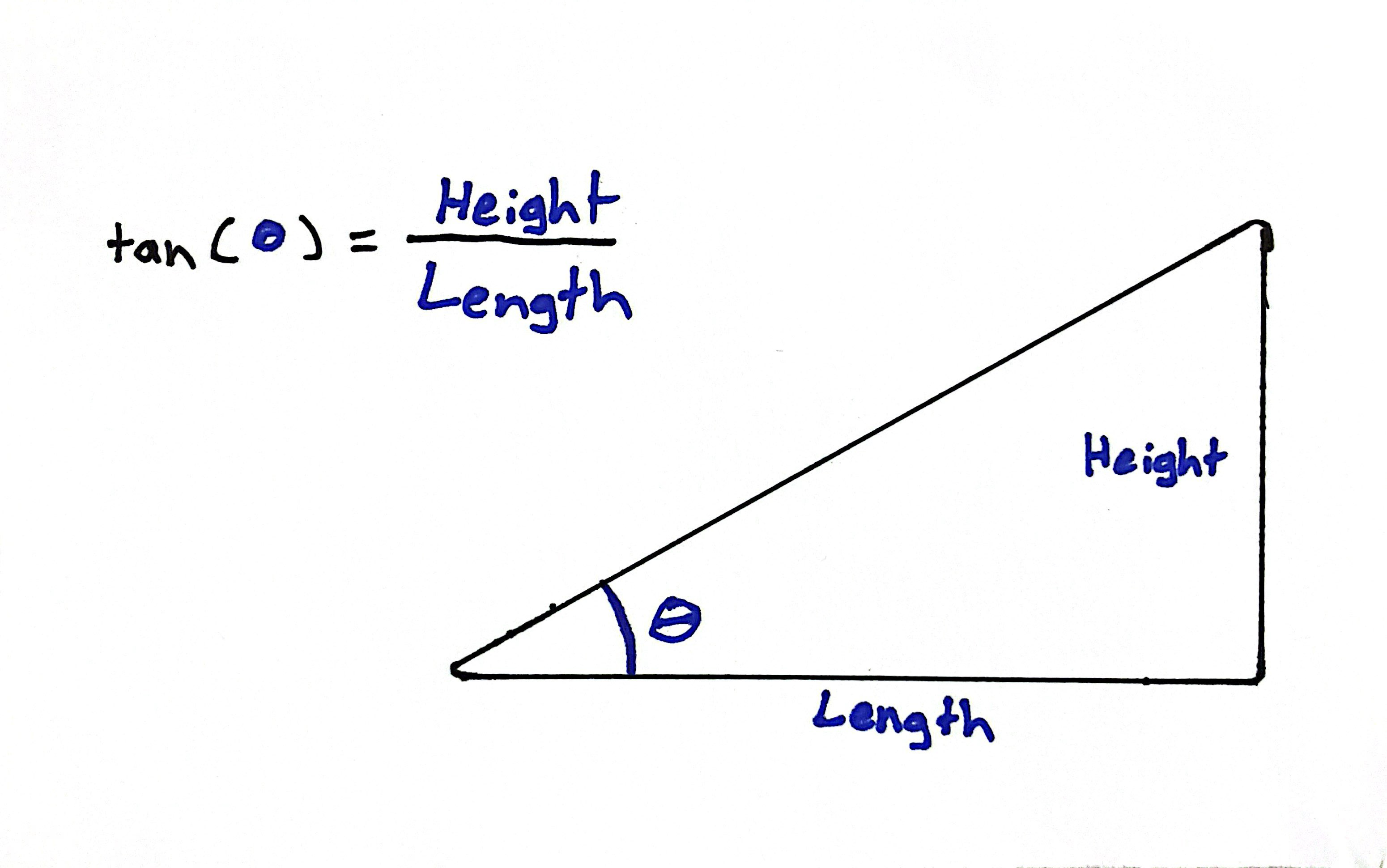 $$\tan (\theta) = \frac{\text{height}}{\text{length}}$$
Solving for length.
$$\text{length}=\frac{\text{height}}{\tan(\theta)}$$
$$\frac{1000\text{ft}}{\tan(3°)}=19,081\text{ft}$$
Converting feet to nautical miles:
\[19,081\text{ft}\cdot\frac{1nm}{6,076\text{ft}}=3.14nm\approx3nm\]
We must be stable on the lateral profile at 3nm.
$$\tan (\theta) = \frac{\text{height}}{\text{length}}$$
Solving for length.
$$\text{length}=\frac{\text{height}}{\tan(\theta)}$$
$$\frac{1000\text{ft}}{\tan(3°)}=19,081\text{ft}$$
Converting feet to nautical miles:
\[19,081\text{ft}\cdot\frac{1nm}{6,076\text{ft}}=3.14nm\approx3nm\]
We must be stable on the lateral profile at 3nm.
Turn Radius
Turn radius can be determined by:
\[r=\frac{v^2}{11.26\tan(\varphi)}\]
where \(r\) is radius in feet,
\(v\) is velocity in kts,
and \(\varphi\) is bank angle.
Considering the CRJ200, 550, 700, and 900, the fastest maneuvering speed at flaps 30 is 151kts. This comes from a CRJ200 at max landing weight of 47,000lbs. Rounding to 160kts adds margin and provides a standard number for our procedure.
$$\frac{(160\text{kts})^2}{11.26\tan(25°)}=4,876\text{ ft}$$
Converting to nautical miles:
\[4,876\text{ft}\cdot\frac{1\text{nm}}{6,076\text{ft}}=0.80\text{nm}\]
The tightest pattern we could fly would be a 1.6nm downwind, and abeam a 3nm final, make a 25° bank turn, lining up with the runway at exactly 1000'.
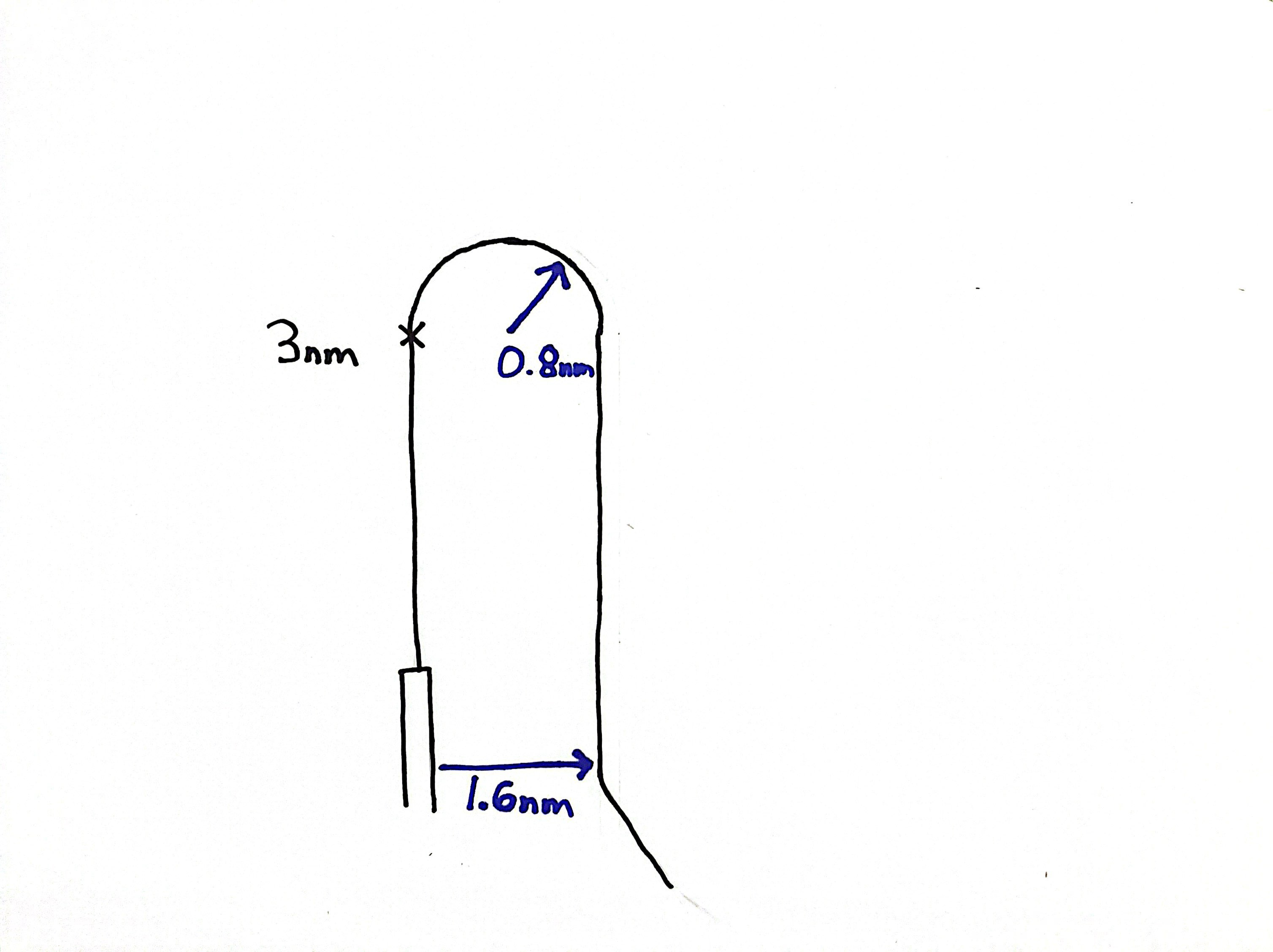
Turn Radius at Altitude
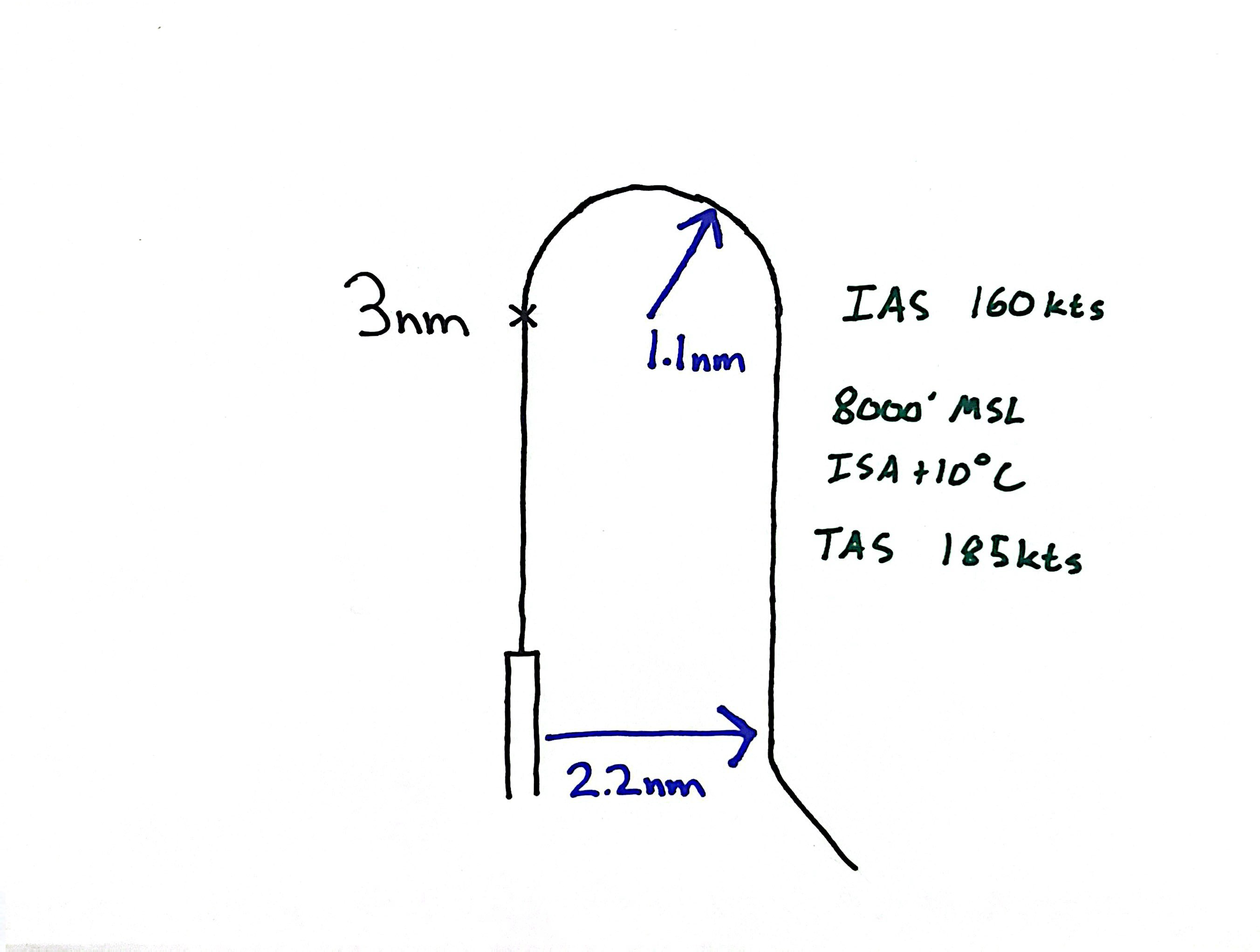
Now we will consider the effect of density altitude on our true airspeed (TAS) compared to our indicated airspeed (IAS).
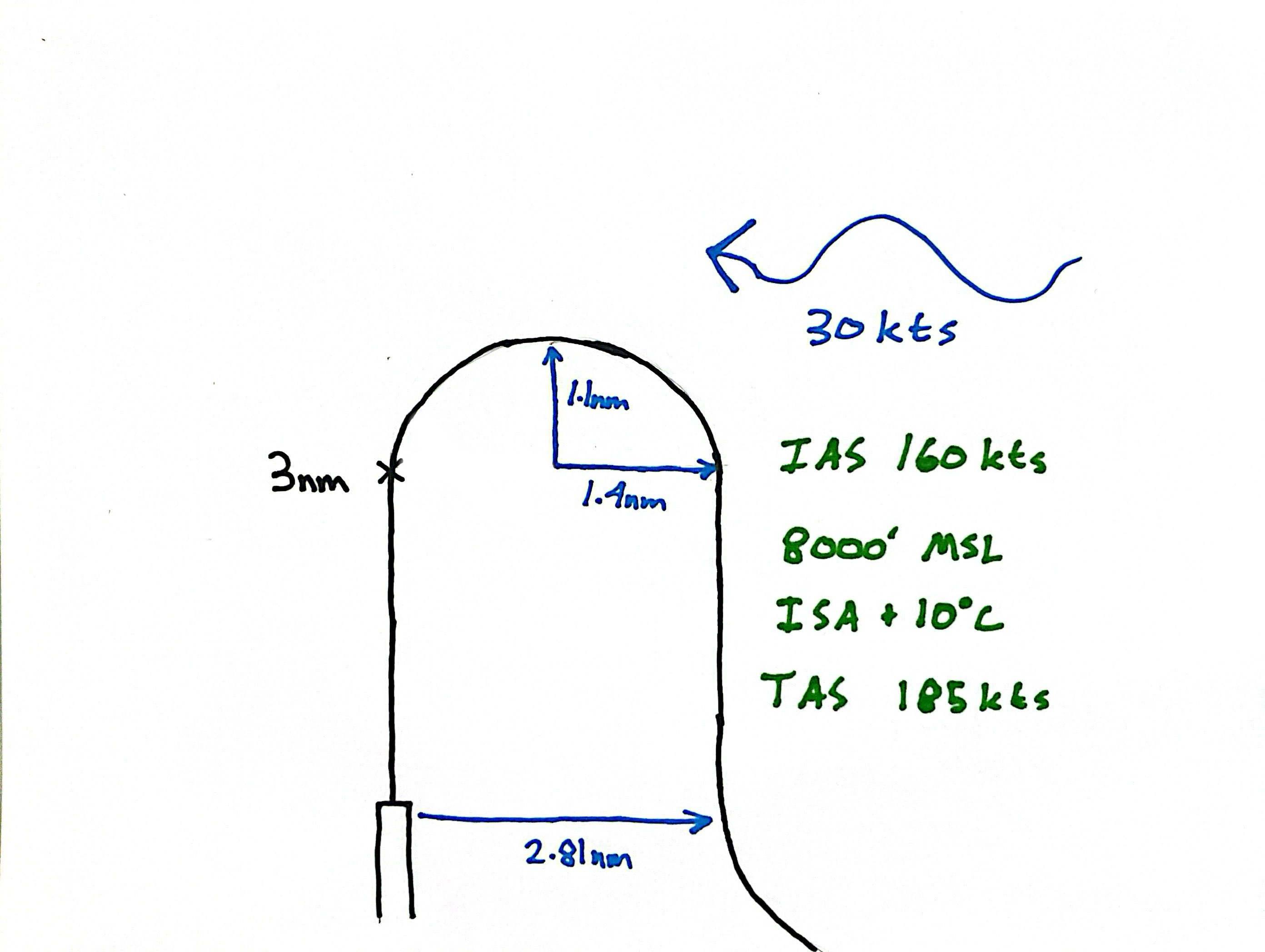
Flying the pattern at 8000' MSL in Durango Colorado on an ISA + 10°C day, 160kts IAS could be as high as 185kts TAS.
$$\frac{(185\text{kts})^2}{11.26\tan(25°)}=6518\text{ft}=1.1\text{nm}$$
Turn diameter has increased from 1.6nm to 2.2nm.
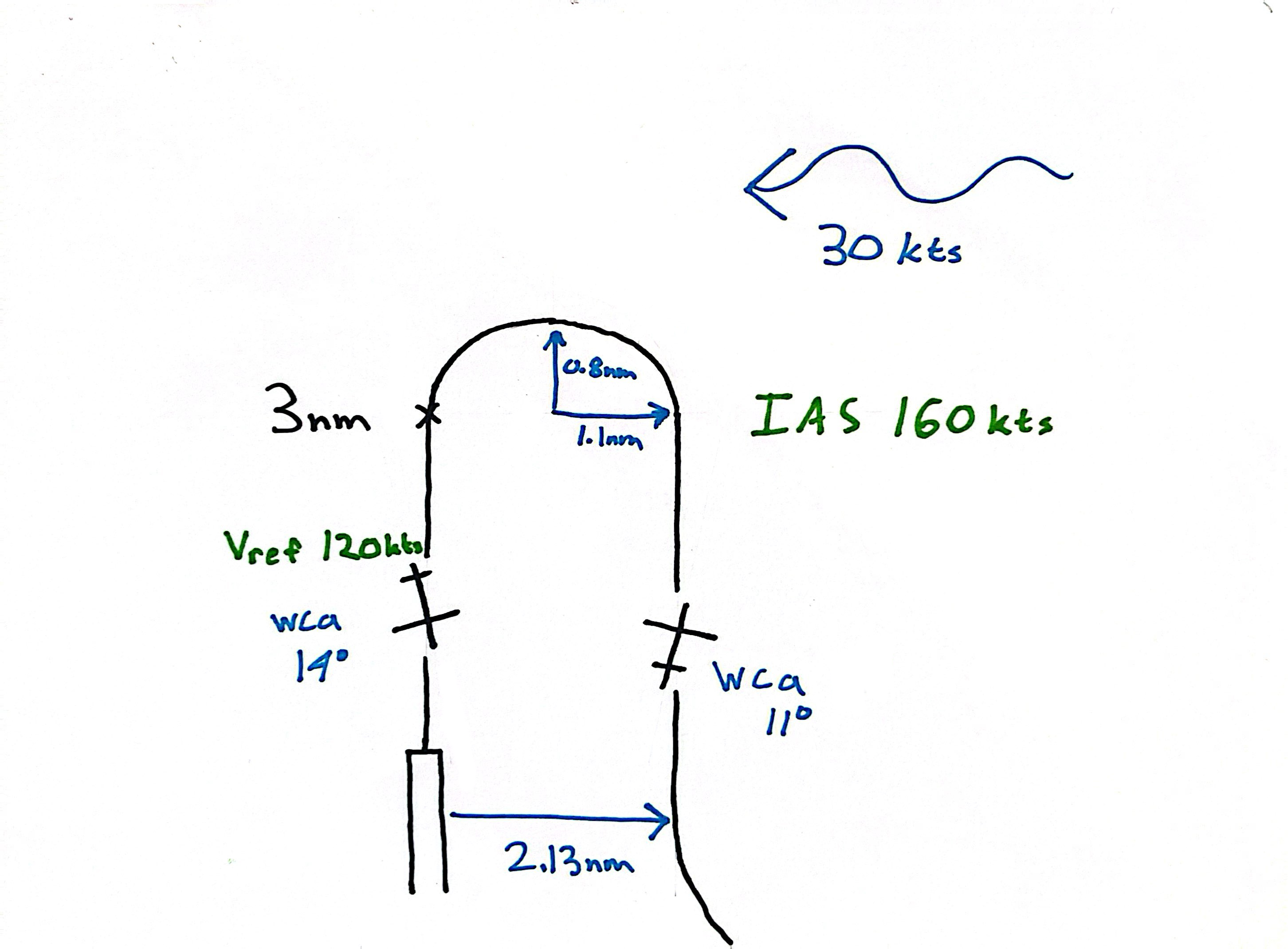
Turn Diameter with a Crosswind
Consider the setup above with a 30kt crosswind from the east.
On downwind, the course is 360° and wind correction angle is 011° right. On final, suppose a Vref of 120kts, the wind correction angle is 14° left.
Therefore, the turn is not a 180° turn, but a 205° turn.
Rate of turn can be expressed as:
$$\omega=\frac{1091\cdot\tan(\theta)}{v}$$
where \(\omega\) is rate of turn in degrees per second,
\(\theta\) is bank angle,
and \(v\) is TAS in kts.
$$\frac{1091\cdot\tan(25^\circ)}{160\text{kts}}=3.18^\circ\text{ per second}$$
The amount of time the aircraft will be exposed to crosswind during the turn is:
$$\frac{205^\circ}{3.18^\circ\text{sec}^{-1}}=64\text{ seconds}$$
30kts converted to nm per second:
$$30\frac{\text{nm}}{\text{hr}}\cdot\frac{1\text{ hr}}{3600\text{ seconds}}=8.3\times10^{-3}\frac{\text{nm}}{\text{sec}}$$
Applied to the duration of the turn:
$$8.3\times10^{-3}\frac{\text{nm}}{\text{sec}}\cdot64\text{ sec}=0.53\text{nm}$$
Our turn width in the case of 30kt crosswind now becomes significantly increased:
$$1.6\text{nm}+0.53\text{nm}=2.13\text{nm}$$
Considering a faster TAS and crosswind:
$$\frac{1091\cdot\tan(25^\circ)}{185\text{kts}}=2.75^\circ\text{ per second}$$
(Wind correction angles are reduced to 9° and 13°.)
$$\frac{180^\circ+9^\circ+13^\circ=202^\circ}{2.75^\circ\text{sec}^{-1}}=73\text{ seconds}$$
$$8.3\times10^{-3}\frac{\text{nm}}{\text{sec}}\cdot73\text{ sec}=0.61\text{nm}$$
$$2.2\text{nm}+0.61\text{nm}=2.81\text{nm}$$
Turn Visibility
The next thing to consider when determining how much distance is required for the downwind to base turn is visibility of the runway from the cockpit.
I know that when I lean into the side window, the farthest back I can see is the aircraft's winglets. Looking at a topdown view of the aircraft with a protractor, I measure 150° on both sides.
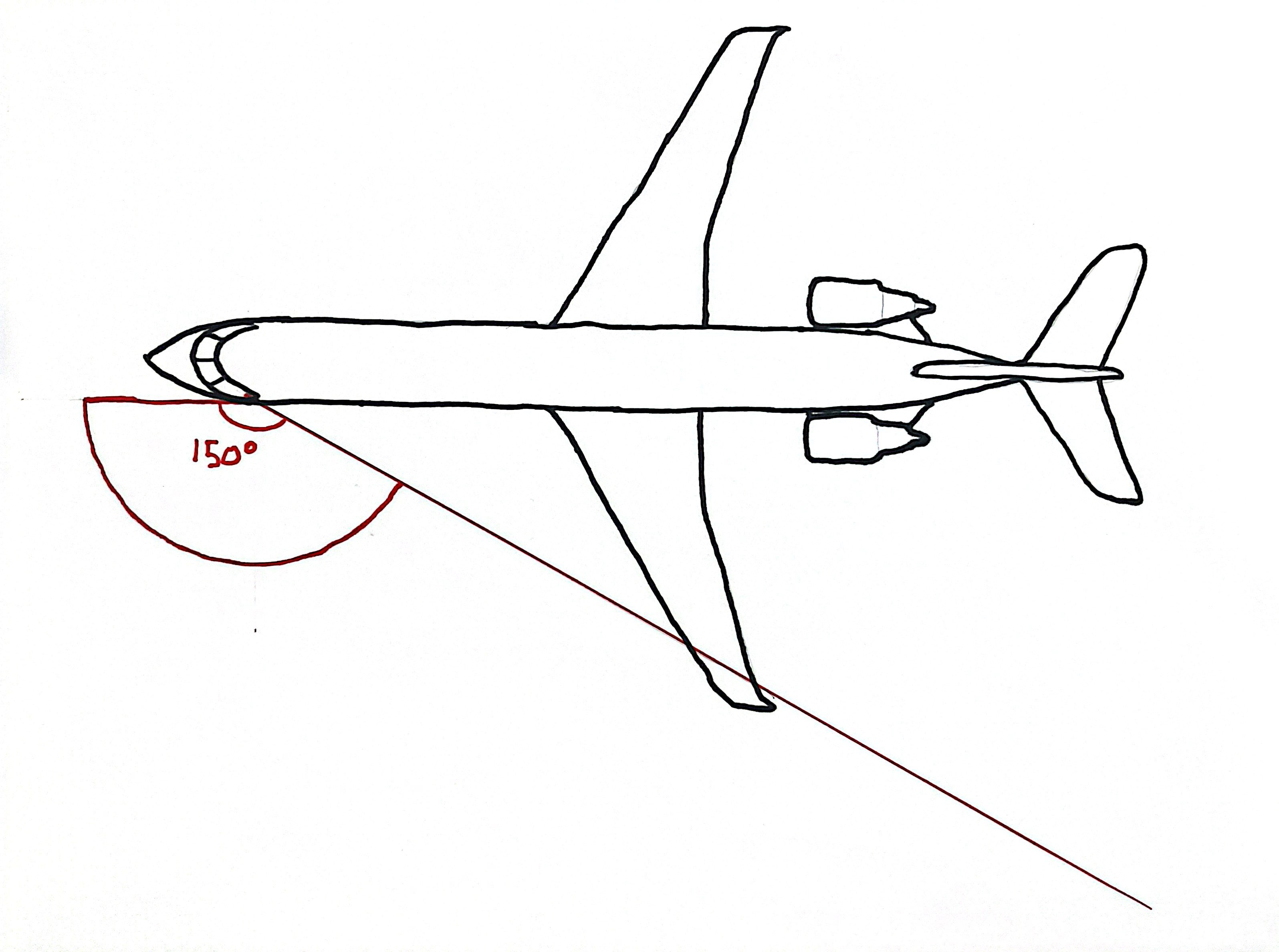
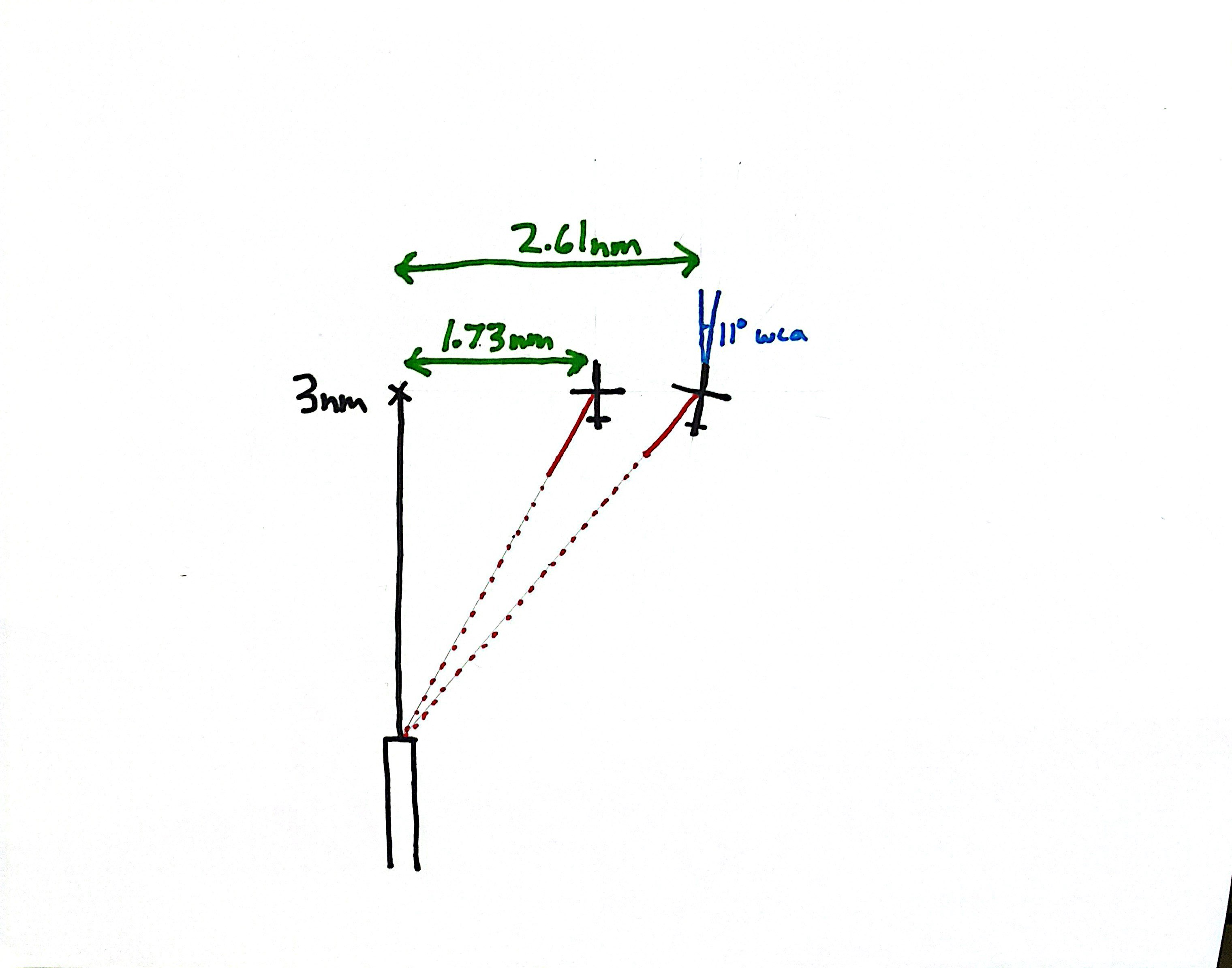
The point of worst visibility occurs on the downwind just before beginning the base turn. Considering a case of no wind. The view angle is 150° therefore the angle from the runway is 30°. On a 3nm downwind, the minimum downwind width before the runway is no longer visible can be calculated as:
$$3\text{nm}\cdot\tan(30^\circ)=1.73\text{nm}$$
And if we account for a wind correction angle of 11°, the view angle is reduced from 150° to 139°. The angle from the runway is now 41°. This requires a distance of:
$$3\text{nm}\cdot\tan(41^\circ)=2.61\text{nm}$$
Sometimes we end up on a longer downwind than 3 miles. In the case of a 5nm downwind, we must be atleast 2.9nm wide or 4.3nm wide in the case of wind.
Conclusion
Flying these patterns would be difficult to execute. The FMS usually deals in whole numbers, however the PROG page does display crosstrack to the nearest tenth of a nautical mile.
The real purpose of this excercise is to understand the limitations of the visual pattern across multiple conditions.
Back
Technique Brief Home
 $$\tan (\theta) = \frac{\text{height}}{\text{length}}$$
Solving for length.
$$\text{length}=\frac{\text{height}}{\tan(\theta)}$$
$$\frac{1000\text{ft}}{\tan(3°)}=19,081\text{ft}$$
Converting feet to nautical miles:
\[19,081\text{ft}\cdot\frac{1nm}{6,076\text{ft}}=3.14nm\approx3nm\]
We must be stable on the lateral profile at 3nm.
$$\tan (\theta) = \frac{\text{height}}{\text{length}}$$
Solving for length.
$$\text{length}=\frac{\text{height}}{\tan(\theta)}$$
$$\frac{1000\text{ft}}{\tan(3°)}=19,081\text{ft}$$
Converting feet to nautical miles:
\[19,081\text{ft}\cdot\frac{1nm}{6,076\text{ft}}=3.14nm\approx3nm\]
We must be stable on the lateral profile at 3nm.





